このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
heaviside
へヴィサイド ステップ関数
説明
例
シンボリック引数または数値引数に対するヘヴィサイド関数の評価
関数 heaviside は引数の値によって 0、1/2、または 1 を返します。引数が浮動小数点数の場合 (シンボリック オブジェクトではない)、heaviside は浮動小数点の結果を返します。
シンボリック入力 sym(-3) について、ヘヴィサイド ステップ関数を評価します。関数 heaviside(x) は x < 0 に対して 0 を返します。
H = heaviside(sym(-3))
H =
シンボリック入力 sym(3) について、ヘヴィサイド ステップ関数を評価します。関数 heaviside(x) は x > 0 に対して 1 を返します。
H = heaviside(sym(3))
H =
シンボリック入力 sym(0) について、ヘヴィサイド ステップ関数を評価します。関数 heaviside(x) は x = 0 に対して 1/2 を返します。
H = heaviside(sym(0))
H =
数値入力 x = 0 に対して、関数 heaviside(x) は浮動小数点の結果を返します。
H = heaviside(0)
H = 0.5000
シンボリック変数の仮定の使用
heaviside は変数についての仮定を考慮に入れます。
シンボリック変数 x を作成し、それが 0 未満であると仮定します。
syms x
assume(x < 0)シンボリック入力 x について、ヘヴィサイド ステップ関数を評価します。
H = heaviside(x)
H =
計算を続けるため、x に設定された仮定を syms を使用して再作成することで消去します。
syms xヘヴィサイド関数のプロット
x および x - 1 のへヴィサイド ステップ関数をプロットします。
syms x
fplot(heaviside(x), [-2, 2])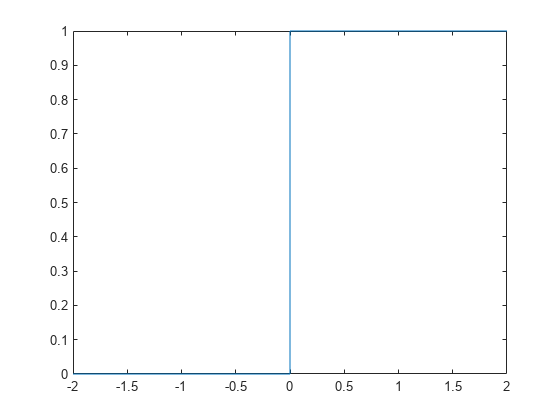
fplot(heaviside(x - 1), [-2, 2])
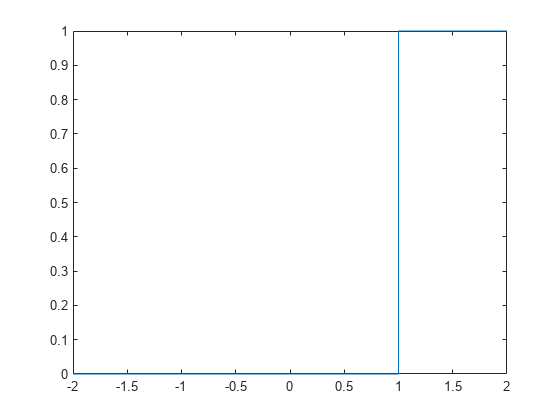
シンボリック行列でのヘヴィサイド関数の評価
シンボリック行列に対するヘヴィサイド関数を評価します。入力引数が行列の場合、heaviside は要素ごとにへヴィサイド関数を計算します。
syms x
H = heaviside(sym([-1 0; 1/2 x]))H =
ヘヴィサイド関数を含む式の微分と積分
へヴィサイド関数を含む式の微分と積分を計算します。
へヴィサイド関数の 1 次導関数を求めます。へヴィサイド関数の 1 次導関数は Dirac のデルタ関数です。
syms x
diff_H = diff(heaviside(x),x)diff_H =
積分 を評価します。
syms x
int_H = int(exp(-x)*heaviside(x),x,-Inf,Inf)int_H =
ヘヴィサイド関数の原点における値の変化
原点におけるヘヴィサイド関数の既定値は 1/2 です。
H = heaviside(sym(0))
H =
その他の、原点におけるヘヴィサイド関数の一般的な値は 0 と 1 です。原点における heaviside の値を変更するには、sympref を使用して 'HeavisideAtOrigin' の値を設定します。sympref によって返された以前のパラメーター値を、後でその値に戻せるように保存します。
oldparam = sympref('HeavisideAtOrigin',1);0 における heaviside の新しい値を確認します。
H = heaviside(sym(0))
H =
sympref によって指定された設定は、これ以降の MATLAB® セッションを通じて維持されます。原点における heaviside の以前の値を戻すには、oldparam に保存されている値を使用します。
sympref('HeavisideAtOrigin',oldparam);または、'default' 設定を使用して 'HeavisideAtOrigin' の既定値に戻すこともできます。
sympref('HeavisideAtOrigin','default');
入力引数
x — 入力
数値 | シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | シンボリック ベクトル | シンボリック行列
入力。数値、シンボリック数、シンボリック変数、シンボリック式、シンボリック関数、シンボリック ベクトルまたはシンボリック行列として指定します。
バージョン履歴
R2006a より前に導入
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)