ガウス・ラゲール求積の評価点と重み

この例では、Symbolic Math Toolbox™ を使って多項方程式と方程式系を解き、その結果を処理する方法を説明します。

ガウス求積法は、和による積分の近似 $\int_{a}^{b} f (t) w (t) d t \approx \sum_{i = 1}^{n} f (x_{i}) α_{i}$ です。ここで、 $x_{i}$ および $α_{i}$ は方式のパラメーターで、 $n$ に依存しますが、 $f$ には依存しません。これらは、選択した重み関数 $w (t)$ から次のように得られます。重み関数には直交多項式族が関連しています。多項式の根は評価点 $x_{i}$ です。最後に、重み $α_{i}$ は、低次数の多項式の場合にこの方式が正しくなるという条件で決まります。区間 $[0, \infty]$ での重み関数 $w (t) = \exp (- t)$ を考えます。これはガウス・ラゲール求積として知られています。

syms t
n = 4;
w(t) = exp(-t);

直交多項式族の最初の $n$ メンバーがわかっているとします。ここで考慮されている求積法の場合、これらがラゲール多項式であることがわかります。

F = laguerreL(0:n-1, t)

F = 
 $(\begin{array}{c} 1 & 1 - t & \frac{t^{2}}{2} - 2 t + 1 & - \frac{t^{3}}{6} + \frac{3 t^{2}}{2} - 3 t + 1 \end{array})$

$n + 1$ 次多項式である L を考えます。係数は未定です。

X = sym('X', [1, n+1])

X =  $(\begin{array}{c} X_{1} & X_{2} & X_{3} & X_{4} & X_{5} \end{array})$

L = poly2sym(X, t)

L =  $X_{1} t^{4} + X_{2} t^{3} + X_{3} t^{2} + X_{4} t + X_{5}$

ラゲール多項式 F および L の直交関係を方程式系 sys で表現します。

sys = [int(F.*L.*w(t), t, 0, inf) == 0]

sys =  $(\begin{array}{c} 24 X_{1} + 6 X_{2} + 2 X_{3} + X_{4} + X_{5} = 0 & - 96 X_{1} - 18 X_{2} - 4 X_{3} - X_{4} = 0 & 144 X_{1} + 18 X_{2} + 2 X_{3} = 0 & - 96 X_{1} - 6 X_{2} = 0 \end{array})$

多項式のノルムが 1 であるという条件を追加します。

sys = [sys, int(L^2.*w(t), 0, inf) == 1]

sys =  $(\begin{array}{c} 24 X_{1} + 6 X_{2} + 2 X_{3} + X_{4} + X_{5} = 0 & - 96 X_{1} - 18 X_{2} - 4 X_{3} - X_{4} = 0 & 144 X_{1} + 18 X_{2} + 2 X_{3} = 0 & - 96 X_{1} - 6 X_{2} = 0 & 40320 {X_{1}}^{2} + 10080 X_{1} X_{2} + 1440 X_{1} X_{3} + 240 X_{1} X_{4} + 48 X_{1} X_{5} + 720 {X_{2}}^{2} + 240 X_{2} X_{3} + 48 X_{2} X_{4} + 12 X_{2} X_{5} + 24 {X_{3}}^{2} + 12 X_{3} X_{4} + 4 X_{3} X_{5} + 2 {X_{4}}^{2} + 2 X_{4} X_{5} + {X_{5}}^{2} = 1 \end{array})$

L の係数の解を求めます。

S = solve(sys, X)

S = struct with fields:
    X1: [2x1 sym]
    X2: [2x1 sym]
    X3: [2x1 sym]
    X4: [2x1 sym]
    X5: [2x1 sym]

solve は 2 つの解を構造体配列で返します。解を表示します。

structfun(@display, S)

ans = 
 $(\begin{array}{c} - \frac{1}{24} \\ \frac{1}{24} \end{array})$

ans = 
 $(\begin{array}{c} \frac{2}{3} \\ - \frac{2}{3} \end{array})$

ans = 
 $(\begin{array}{c} - 3 \\ 3 \end{array})$

ans = 
 $(\begin{array}{c} 4 \\ - 4 \end{array})$

ans = 
 $(\begin{array}{c} - 1 \\ 1 \end{array})$

最初の係数は正であるという追加の条件を追加して、解を一意にします。

sys = [sys, X(1)>0];
S = solve(sys, X)

S = struct with fields:
    X1: 1/24
    X2: -2/3
    X3: 3
    X4: -4
    X5: 1

解を L に代入します。

L = subs(L, S)

L = 
 $\frac{t^{4}}{24} - \frac{2 t^{3}}{3} + 3 t^{2} - 4 t + 1$

予想どおり、この多項式は |n| 次のラゲール多項式です。

laguerreL(n, t)

ans = 
 $\frac{t^{4}}{24} - \frac{2 t^{3}}{3} + 3 t^{2} - 4 t + 1$

評価点 $x_{i}$ は多項式 L の根です。この評価点について L を解きます。根は、関数 root で表現されます。

x = solve(L)

x = 
 $\begin{array}{l} (\begin{array}{c} root (σ_{1}, z, 1) \\ root (σ_{1}, z, 2) \\ root (σ_{1}, z, 3) \\ root (σ_{1}, z, 4) \end{array}) \\ where \\ σ_{1} = z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24 \end{array}$

これらの解の形式は、何も成立していないことを示している場合もありますが、これらについてのさまざまな演算は利用可能です。vpa を使用して浮動小数点近似を計算します。

vpa(x)

ans = 
 $(\begin{array}{c} 0.32254768961939231180036145910437 \\ 1.7457611011583465756868167125179 \\ 4.5366202969211279832792853849571 \\ 9.3950709123011331292335364434205 \end{array})$

疑似的な虚数部が発生する可能性があります。根が実数であることをシンボリックに証明します。

isAlways(in(x, 'real'))

ans = 4x1 logical array

   1
   1
   1
   1

4 次以下の多項式の場合、MaxDegree を使用して、root ではなく入れ子にされた累乗根で解が得られます。ただし、この形式の結果に対するそれ以降の演算は遅くなります。

xradical = solve(L, 'MaxDegree', 4)

xradical = 
 $\begin{array}{l} (\begin{array}{c} 4 - σ_{1} - σ_{3} \\ 4 + σ_{1} - σ_{3} \\ σ_{3} - σ_{2} + 4 \\ σ_{3} + σ_{2} + 4 \end{array}) \\ where \\ σ_{1} = \frac{\sqrt{96 σ_{6} σ_{4} - 3 σ_{5} σ_{4} - 288 σ_{4} - 512 \sqrt{3} \sqrt{6} \sqrt{6 + \sqrt{3} \sqrt{6} i}}}{2 {(768 + 128 \sqrt{3} \sqrt{6} i)}^{1 / 6} {(144 σ_{6} + 9 σ_{5} + 864)}^{1 / 4}} \\ σ_{2} = \frac{\sqrt{96 σ_{6} σ_{4} - 3 σ_{5} σ_{4} - 288 σ_{4} + 512 \sqrt{3} \sqrt{6} \sqrt{6 + \sqrt{3} \sqrt{6} i}}}{2 {(768 + 128 \sqrt{3} \sqrt{6} i)}^{1 / 6} {(144 σ_{6} + 9 σ_{5} + 864)}^{1 / 4}} \\ σ_{3} = \frac{σ_{4}}{2 {(768 + 128 \sqrt{3} \sqrt{6} i)}^{1 / 6}} \\ σ_{4} = \sqrt{16 σ_{6} + σ_{5} + 96} \\ σ_{5} = {(768 + 128 \sqrt{3} \sqrt{6} i)}^{2 / 3} \\ σ_{6} = {(768 + 128 \sqrt{3} \sqrt{6} i)}^{1 / 3} \end{array}$

重み $α_{i}$ は、多項式が $n$ 次未満の場合、求積法により必ず厳密な結果を得られるという条件で与えられます。これがこれらの多項式のベクトル空間の基底に当てはまる場合には、これで十分です。この条件は、4 変数の 4 つの方程式から成る系になります。

y = sym('y', [n, 1]);
sys = sym(zeros(n));
for k=0:n-1 
    sys(k+1) = sum(y.*(x.^k)) == int(t^k * w(t), t, 0, inf); 
end
sys

sys = 
 $\begin{array}{l} (\begin{array}{c} y_{1} + y_{2} + y_{3} + y_{4} = 1 & 0 & 0 & 0 \\ y_{1} root (σ_{1}, z, 1) + y_{2} root (σ_{1}, z, 2) + y_{3} root (σ_{1}, z, 3) + y_{4} root (σ_{1}, z, 4) = 1 & 0 & 0 & 0 \\ y_{1} {root (σ_{1}, z, 1)}^{2} + y_{2} {root (σ_{1}, z, 2)}^{2} + y_{3} {root (σ_{1}, z, 3)}^{2} + y_{4} {root (σ_{1}, z, 4)}^{2} = 2 & 0 & 0 & 0 \\ y_{1} {root (σ_{1}, z, 1)}^{3} + y_{2} {root (σ_{1}, z, 2)}^{3} + y_{3} {root (σ_{1}, z, 3)}^{3} + y_{4} {root (σ_{1}, z, 4)}^{3} = 6 & 0 & 0 & 0 \end{array}) \\ where \\ σ_{1} = z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24 \end{array}$

数値的およびシンボリックに系を解きます。解は重み $α_{i}$ の目的のベクトルです。

[a1, a2, a3, a4] = vpasolve(sys, y)

a1 =  $0.60315410434163360163596602381808$

a2 =  $0.35741869243779968664149201745809$

a3 =  $0.03888790851500538427243816815621$

a4 =  $0.00053929470556132745010379056762059$

[alpha1, alpha2, alpha3, alpha4] = solve(sys, y)

alpha1 = 
 $\begin{array}{l} - \frac{σ_{3} σ_{2} + σ_{3} σ_{1} + σ_{2} σ_{1} - σ_{3} σ_{2} σ_{1} - 2 σ_{3} - 2 σ_{2} - 2 σ_{1} + 6}{(σ_{4} - σ_{3}) (σ_{4} σ_{2} + σ_{4} σ_{1} - σ_{2} σ_{1} - {σ_{4}}^{2})} \\ where \\ σ_{1} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 4) \\ σ_{2} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 3) \\ σ_{3} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 2) \\ σ_{4} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 1) \end{array}$

alpha2 = 
 $\begin{array}{l} \frac{root (σ_{1}, z, 1) root (σ_{1}, z, 3) + root (σ_{1}, z, 1) root (σ_{1}, z, 4) + root (σ_{1}, z, 3) root (σ_{1}, z, 4) - root (σ_{1}, z, 1) root (σ_{1}, z, 3) root (σ_{1}, z, 4) - 2 root (σ_{1}, z, 1) - 2 root (σ_{1}, z, 3) - 2 root (σ_{1}, z, 4) + 6}{(root (σ_{1}, z, 2) - root (σ_{1}, z, 1)) (root (σ_{1}, z, 2) - root (σ_{1}, z, 3)) (root (σ_{1}, z, 2) - root (σ_{1}, z, 4))} \\ where \\ σ_{1} = z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24 \end{array}$

alpha3 = 
 $\begin{array}{l} \frac{σ_{3} σ_{2} + σ_{3} σ_{1} + σ_{2} σ_{1} - σ_{3} σ_{2} σ_{1} - 2 σ_{3} - 2 σ_{2} - 2 σ_{1} + 6}{(σ_{4} - σ_{1}) (σ_{3} σ_{2} - σ_{3} σ_{4} - σ_{2} σ_{4} + {σ_{4}}^{2})} \\ where \\ σ_{1} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 4) \\ σ_{2} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 2) \\ σ_{3} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 1) \\ σ_{4} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 3) \end{array}$

alpha4 = 
 $\begin{array}{l} - \frac{σ_{3} σ_{2} + σ_{3} σ_{1} + σ_{2} σ_{1} - σ_{3} σ_{2} σ_{1} - 2 σ_{3} - 2 σ_{2} - 2 σ_{1} + 6}{{σ_{4}}^{2} σ_{3} + {σ_{4}}^{2} σ_{2} + {σ_{4}}^{2} σ_{1} - {σ_{4}}^{3} + σ_{3} σ_{2} σ_{1} - σ_{3} σ_{2} σ_{4} - σ_{3} σ_{1} σ_{4} - σ_{2} σ_{1} σ_{4}} \\ where \\ σ_{1} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 3) \\ σ_{2} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 2) \\ σ_{3} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 1) \\ σ_{4} = root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 4) \end{array}$

また、出力引数を 1 つだけ指定することで、解を構造体として得ることもできます。

S = solve(sys, y)

S = struct with fields:
    y1: -(root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 3) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 4) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 3)*root(z...
    y2: (root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 3) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 4) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 3)*root(z^...
    y3: (root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 4) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2)*root(z^...
    y4: -(root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 1)*root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 3) + root(z^4 - 16*z^3 + 72*z^2 - 96*z + 24, z, 2)*root(z...

structfun(@double, S)

構造体 S をシンボリック配列に変換します。

Scell = struct2cell(S);
alpha = transpose([Scell{:}])

alpha = 
 $\begin{array}{l} (\begin{array}{c} - \frac{σ_{3} + σ_{15} + σ_{2} - σ_{6} - σ_{12} - σ_{11} - σ_{10} + 6}{(root (σ_{16}, z, 1) - root (σ_{16}, z, 2)) (σ_{1} + σ_{4} - σ_{2} - {root (σ_{16}, z, 1)}^{2})} \\ \frac{σ_{1} + σ_{4} + σ_{2} - σ_{7} - σ_{13} - σ_{11} - σ_{10} + 6}{(root (σ_{16}, z, 2) - root (σ_{16}, z, 1)) (root (σ_{16}, z, 2) - root (σ_{16}, z, 3)) (root (σ_{16}, z, 2) - root (σ_{16}, z, 4))} \\ \frac{σ_{5} + σ_{4} + σ_{15} - σ_{8} - σ_{13} - σ_{12} - σ_{10} + 6}{(root (σ_{16}, z, 3) - root (σ_{16}, z, 4)) (σ_{5} - σ_{1} - σ_{3} + {root (σ_{16}, z, 3)}^{2})} \\ - \frac{σ_{5} + σ_{1} + σ_{3} - σ_{9} - σ_{13} - σ_{12} - σ_{11} + 6}{σ_{14} root (σ_{16}, z, 1) + σ_{14} root (σ_{16}, z, 2) + σ_{14} root (σ_{16}, z, 3) - {root (σ_{16}, z, 4)}^{3} + σ_{9} - σ_{8} - σ_{7} - σ_{6}} \end{array}) \\ where \\ σ_{1} = root (σ_{16}, z, 1) root (σ_{16}, z, 3) \\ σ_{2} = root (σ_{16}, z, 3) root (σ_{16}, z, 4) \\ σ_{3} = root (σ_{16}, z, 2) root (σ_{16}, z, 3) \\ σ_{4} = root (σ_{16}, z, 1) root (σ_{16}, z, 4) \\ σ_{5} = root (σ_{16}, z, 1) root (σ_{16}, z, 2) \\ σ_{6} = root (σ_{16}, z, 2) root (σ_{16}, z, 3) root (σ_{16}, z, 4) \\ σ_{7} = root (σ_{16}, z, 1) root (σ_{16}, z, 3) root (σ_{16}, z, 4) \\ σ_{8} = root (σ_{16}, z, 1) root (σ_{16}, z, 2) root (σ_{16}, z, 4) \\ σ_{9} = root (σ_{16}, z, 1) root (σ_{16}, z, 2) root (σ_{16}, z, 3) \\ σ_{10} = 2 root (σ_{16}, z, 4) \\ σ_{11} = 2 root (σ_{16}, z, 3) \\ σ_{12} = 2 root (σ_{16}, z, 2) \\ σ_{13} = 2 root (σ_{16}, z, 1) \\ σ_{14} = {root (σ_{16}, z, 4)}^{2} \\ σ_{15} = root (σ_{16}, z, 2) root (σ_{16}, z, 4) \\ σ_{16} = z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24 \end{array}$

シンボリックな解は複雑に見えます。これを単純化し、浮動小数点ベクトルに変換します。

alpha = simplify(alpha)

alpha = 
 $\begin{array}{l} (\begin{array}{c} \frac{{root (σ_{1}, z, 1)}^{2}}{72} - \frac{29 root (σ_{1}, z, 1)}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z, 2)}^{2}}{72} - \frac{29 root (σ_{1}, z, 2)}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z, 3)}^{2}}{72} - \frac{29 root (σ_{1}, z, 3)}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z, 4)}^{2}}{72} - \frac{29 root (σ_{1}, z, 4)}{144} + \frac{2}{3} \end{array}) \\ where \\ σ_{1} = z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24 \end{array}$

vpa(alpha)

ans = 
 $(\begin{array}{c} 0.60315410434163360163596602381808 \\ 0.35741869243779968664149201745809 \\ 0.03888790851500538427243816815621 \\ 0.00053929470556132745010379056762059 \end{array})$

alpha に現れる根 x を略語に置き換えて、可読性を高めます。

subs(alpha, x, sym('R', [4, 1]))

ans = 
 $\begin{array}{l} (\begin{array}{c} \frac{{R_{1}}^{2}}{72} - \frac{29 R_{1}}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z_{1}, 2)}^{2}}{72} - \frac{29 root (σ_{1}, z_{1}, 2)}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z_{1}, 3)}^{2}}{72} - \frac{29 root (σ_{1}, z_{1}, 3)}{144} + \frac{2}{3} \\ \frac{{root (σ_{1}, z_{1}, 4)}^{2}}{72} - \frac{29 root (σ_{1}, z_{1}, 4)}{144} + \frac{2}{3} \end{array}) \\ where \\ σ_{1} = {z_{1}}^{4} - 16 {z_{1}}^{3} + 72 {z_{1}}^{2} - 96 z_{1} + 24 \end{array}$

重みを合計して和が 1 であることを示します。

simplify(sum(alpha))

ans =  $1$

求積法の重みを求める別の方法は、式 $α_{i} = \int_{a}^{b} w (t) \prod_{j \neq i} \frac{t - x_{j}}{x_{i} - x_{j}} d t$ を使用して計算することです。 $i = 1$ でこれを行います。これは、次のように別の方法と同じ結果となります。

int(w(t) * prod((t - x(2:4)) ./ (x(1) - x(2:4))), t, 0, inf)

ans = 
 $\frac{{root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 1)}^{2}}{72} - \frac{29 root (z^{4} - 16 z^{3} + 72 z^{2} - 96 z + 24, z, 1)}{144} + \frac{2}{3}$

求積法では、 $2 n - 1$ 次以下のすべての多項式に対しても厳密な結果が得られますが、 $t^{2 n}$ に対しては得られません。

simplify(sum(alpha.*(x.^(2*n-1))) -int(t^(2*n-1)*w(t), t, 0, inf))

ans =  $0$

simplify(sum(alpha.*(x.^(2*n))) -int(t^(2*n)*w(t), t, 0, inf))

ans =  $- 576$

余弦に求積法を適用し、厳密な結果と比較します。

vpa(sum(alpha.*(cos(x))))

ans =  $0.50249370546067059229918484198931$

int(cos(t)*w(t), t, 0, inf)

ans = 
 $\frac{1}{2}$

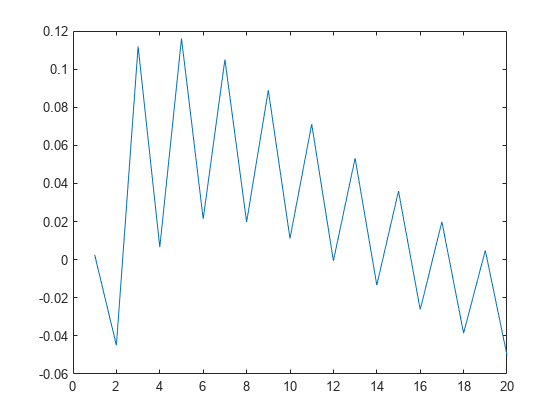
余弦のべき乗では、奇数乗と偶数乗の間で誤差が振動します。

errors = zeros(1, 20);
for k=1:20 
    errors(k) = double(sum(alpha.*(cos(x).^k)) -int(cos(t)^k*w(t), t, 0, inf));
end
plot(real(errors))

Figure contains an axes object. The axes object contains an object of type line.