このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
bernstein
バーンスタイン多項式
説明
関数ハンドル f をもつ bernstein( は、f,n,t)t 点において評価された n 次のバーンスタイン多項式 symsum(nchoosek(n,k)*t^k*(1-t)^(n-k)*f(k/n),k,0,n) を返します。この多項式は、区間 [0,1] における関数 f を近似します。
例
関数ハンドルとして指定される正弦関数の近似
10 次および 100 次のバーンスタイン多項式で正弦関数を近似します。
syms t
b10 = bernstein(@(t) sin(2*pi*t), 10, t);
b100 = bernstein(@(t) sin(2*pi*t), 100, t);sin(2*pi*t) とその近似をプロットします。
fplot(sin(2*pi*t),[0,1]) hold on fplot(b10,[0,1]) fplot(b100,[0,1]) legend('sine function','10th-degree polynomial',... '100th-degree polynomial') title('Bernstein polynomials') hold off
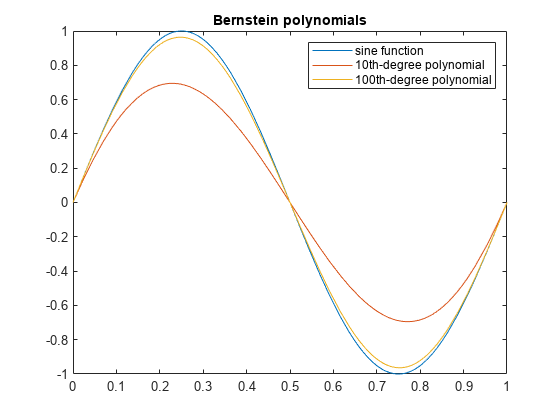
シンボリック式として指定される指数関数の近似
指数関数を変数 t の 2 次のバーンスタイン多項式で近似します。
syms x t bernstein(exp(x), 2, t)
ans = (t - 1)^2 + t^2*exp(1) - 2*t*exp(1/2)*(t - 1)
多変数指数関数を近似します。多変数関数を近似する場合、bernstein はこの関数を symvar によって決まる既定の変数の一変数関数として認識します。式 y*exp(x*y) の既定の変数は x です。
syms x y t symvar(y*exp(x*y), 1)
ans = x
bernstein はこの式を x の一変数関数と見なします。
bernstein(y*exp(x*y), 2, t)
ans = y*(t - 1)^2 + t^2*y*exp(y) - 2*t*y*exp(y/2)*(t - 1)
y*exp(x*y) を変数 y の関数として扱うには、変数を明示的に指定します。
bernstein(y*exp(x*y), y, 2, t)
ans = t^2*exp(x) - t*exp(x/2)*(t - 1)
シンボリック関数として指定される直線傾斜の近似
直線傾斜を表す関数 f を変数 t の 5 次のバーンスタイン多項式で近似します。
syms f(t) f(t) = triangularPulse(1/4, 3/4, Inf, t); p = bernstein(f, 5, t)
p = 7*t^3*(t - 1)^2 - 3*t^2*(t - 1)^3 - 5*t^4*(t - 1) + t^5
結果を単純化します。
simplify(p)
ans = -t^2*(2*t - 3)
単純化されたバーンスタイン多項式の数値安定性
シンボリックな高階数のバーンスタイン多項式を単純化すると、数値的に安定した方法で結果を評価できないことがよくあります。
この矩形パルス関数を 100 次のバーンスタイン多項式で近似し、その結果を単純化します。
f = @(x)rectangularPulse(1/4,3/4,x);
b1 = bernstein(f, 100, sym('t'));
b2 = simplify(b1);多項式 b1 と単純化した多項式 b2 を MATLAB® 関数に変換します。
f1 = matlabFunction(b1); f2 = matlabFunction(b2);
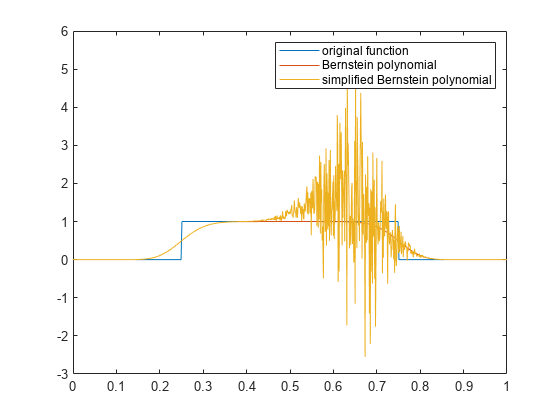
元の矩形パルス関数、数値的に安定したバーンスタイン多項式表現 f1 および単純化版の f2 のプロットを比較してみてください。単純化版は数値的に安定していません。
t = 0:0.001:1; plot(t, f(t), t, f1(t), t, f2(t)) hold on legend('original function','Bernstein polynomial',... 'simplified Bernstein polynomial') hold off
入力引数
詳細
ヒント
シンボリックな
tに対して返されるシンボリック多項式は、tに対して0から1の間の数値を代入する場合、数値的に安定しています。シンボリックなバーンスタイン多項式を単純化すると、曲線のパラメーター
tに対して数値を代入した場合に結果が不安定になることがあります。
バージョン履歴
R2013b で導入
参考
bernsteinMatrix | formula | nchoosek | symvar | symsum
