一般化パレート分布
定義
形状パラメーター k ≠ 0、スケール パラメーター σ、限界値パラメーター θ をもつ一般化パレート分布の確率密度関数は、次の式で表されます。
k > 0 の場合、θ < x です。または k < 0 の場合、θ < x < θ – σ/k です。
k = 0 の場合、密度は θ < x について次のようになります。
k = 0 かつ θ = 0 の場合、作成されたパレート分布は指数分布になります。k > 0 および θ = σ/k である一般化パレート分布は、スケール パラメーターが σ/k、形状パラメーターが 1/k であるパレート分布に等しくなります。
背景
指数分布のように、一般化パレート分布は、他の分布の裾をモデル化するのに使用される場合がしばしばあります。たとえば、製造工程からのワッシャーがあるとします。工程のランダムな影響によって、ワッシャーのサイズに違いが生じる場合は、これらのサイズのモデル化に正規分布のような標準の確率分布を使用できます。ただし、正規分布は、最頻値の近くでは良いモデルであっても、裾では実際のデータへの当てはめが適していないこともあり、すべての範囲のデータを記述するには、より複雑なモデルが必要になることがあります。一方、あるしきい値よりも大きい (または小さい) ワッシャーのサイズのみ記録することは、"超過"と考えられる、これらの裾のデータに異なるモデルを当てはめできることを意味します。このような場合に一般化パレート分布を使用すると、複雑なデータの極端な部分を適切に近似できます。
一般化パレート分布によって、特別な場合として指数分布とパレート分布の両方を含む、可能な形状の連続する範囲が実現します。これらの分布のいずれかを使用して、超過の特定のデータセットをモデル化できます。一般化パレート分布により、どの分布が適切であるかを「データに決めさせる」ことができます。
一般化パレート分布には 3 つの基本的な形式があり、それぞれが、基準となる分布の別のクラスから派生した超過データの極限分布に該当します。
正規分布のように、両裾が指数減衰する分布は、形状パラメーターがゼロの一般化パレート分布になります。
スチューデントの t 分布のように、多項式減衰する裾をもつ分布は、正の形状パラメーターをもちます。
ベータ分布のように、分布の裾が有限の場合は、負の形状パラメーターをもちます。
一般化パレート分布は paretotails オブジェクトの分布近似オブジェクトの裾で使用されます。
パラメーター
一般化パレート分布の当てはめ
自由度 5 のスチューデントの "t" 分布から取り出された多数の乱数値を生成し、2 より小さい値を破棄します。それらの超過に一般化パレート分布を当てはめます。
rng("default") % For reproducibility t = trnd(5,5000,1); y = t(t > 2) - 2; paramEsts = gpfit(y)
paramEsts = 1×2
0.1445 0.7225
スチューデントの t 分布を超過するデータに基づき推測する、形状パラメーターの推定 (最初の要素) は正であることに注意してください。
h = histogram(y+2,2:0.5:12);
h.FaceColor = [0.8 0.8 1];
xgrid = linspace(2,12,1000);
line(xgrid,0.5*length(y)* ...
gppdf(xgrid,paramEsts(1),paramEsts(2),2));
xlim([2 12])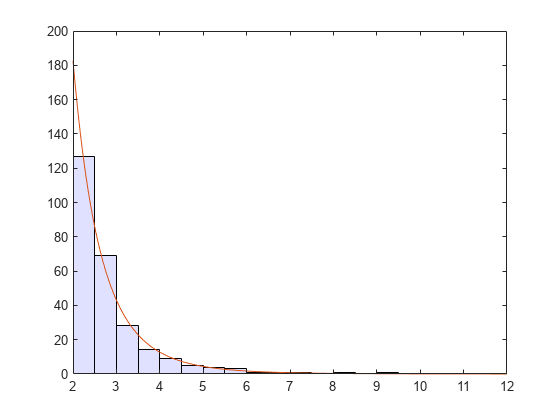
例
一般化パレート分布の確率密度関数の計算
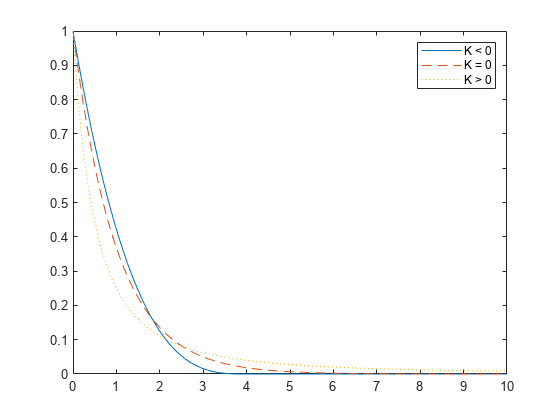
3 つの一般化パレート分布の確率密度関数を計算します。最初の関数の形状パラメーターは k = -0.25、2 番目の分布は k = 0、3 番目の分布は k = 1 です。
x = linspace(0,10,1000); y1 = gppdf(x,-.25,1,0); y2 = gppdf(x,0,1,0); y3 = gppdf(x,1,1,0);
3 つの確率密度関数を同じ Figure にプロットします。
figure; plot(x,y1,'-', x,y2,'--', x,y3,':') legend({'K < 0' 'K = 0' 'K > 0'});
参照
[1] Embrechts, P., C. Klüppelberg, and T. Mikosch. Modelling Extremal Events for Insurance and Finance. New York: Springer, 1997.
[2] Kotz, S., and S. Nadarajah. Extreme Value Distributions: Theory and Applications. London: Imperial College Press, 2000.
