Flexible Shaft
Shaft with torsional and bending compliance
Libraries:
Simscape /
Driveline /
Couplings & Drives
Description
The Flexible Shaft block represents a driveline shaft with torsional and bending compliance. The shaft consists of a flexible material that twists in response to an applied torque and bends in response to static mass unbalance. The twisting action delays power transmission between the shaft ends, altering the dynamic response of the driveline system.

To represent a torsion-flexible shaft, the block uses a lumped mass method. This model divides the shaft into different elements that interconnect through parallel spring damper systems. The elements provide the shaft inertia while the spring damper systems provide the shaft compliance.
The block provides four parameterization methods that allow you to model compliance in either a homogeneous or an axially inhomogeneous shaft. An axially inhomogeneous shaft is one for which any of these attributes vary along the length of the shaft:
Torsional stiffness
Torsional inertia
Bending rigidity
Density
Shear modulus
Young's modulus
Outer diameter
Inner diameter
An additional parameter enables you to model the power losses in the bearings due to viscous friction at the shaft ends. For more information, see Torsion Model.
Note
The viscous friction at the shaft ends is different from the internal material damping, which corresponds to losses arising in the shaft material itself.
To represent the bending-flexible shaft, the block uses either a lumped mass method or an eigenmodes method. While the lumped mass method is simpler to configure, the eigenmodes method tends to simulate faster.
Tip
To prioritize simulation speed, first simulate using the lumped mass method, adjusting parameters as needed until the results match your mathematical models or experimental data. Next, simulate using the eigenmodes method. Again, adjust the parameters as needed until the results mathematical models or experimental data. For an example that uses both methods, see Shaft with Torsional and Transverse Flexibility.
For the lumped mass method, the number of bending shaft elements is the same as the number of torsion shaft elements. The model divides the shaft into a series of such elements. The elements provide the shaft inertia, while the stiffness matrices provide the shaft compliance. The eigenmodes method computes effective mass-spring-damper systems that represent the bending modes of the shaft. You can specify the number of modes to include and the precision of the mode shapes. Both the lumped mass and eigenmodes methods allow you to model:
Excitational static unbalances
Concentrically attached rigid masses
Up to four support locations along the shaft
Linear damping proportional to shaft inertia
Linear damping proportional to shaft stiffness
Note
The eigenmodes method assumes that the support damping is light compared to support stiffness.
Static unbalances, which excite bending, occur when the center of mass of the shaft or an attached rigid mass is not aligned with the shaft principal axis. You can vary the locations, magnitudes, and angle offsets of static unbalances on the shaft.
You can represent concentrically attached rigid masses as disks or idealized point masses. A concentric disk adds diametric and polar moments of inertia to the shaft and mass to the translation degree of freedom of the shaft nodes. The model assumes that the disk is thin, so the shaft can still bend on either side of the axial location with the disk. The polar moment of inertia couples the two planes of bending. A concentric point mass is an idealized version of a concentric disk. A concentric point mass adds mass to the translation degrees of freedom of the shaft nodes but does not have rotational moments of inertia. You can vary the locations and inertias of concentric disks or point masses that are attached to the shaft.
You can model the supports as ideal or by using stiffness and damping matrices. For each support, you can vary the:
Location — Any point along the shaft length.
Type — Ideal clamp, ideal pin, free, constant bearing stiffness and damping, or speed-dependent stiffness and damping.
Number — Two, three, or four.
For both bending methods, you can specify the shaft bending compliance by using either bending rigidity and linear mass density or Young’s modulus and shaft diameter.
You can parameterize the torsional model by using either stiffness k and inertia J or the dimensions and material properties of the shaft.
Torsion Model
For the torsion model, the Flexible Shaft block approximates the distributed, continuous properties of a shaft by using a lumped mass method. The model contains a finite number, N, of lumped inertia-damped spring elements in series, plus a final inertia. The result is a series of inertias connected by N rotational springs and N rotational dampers.
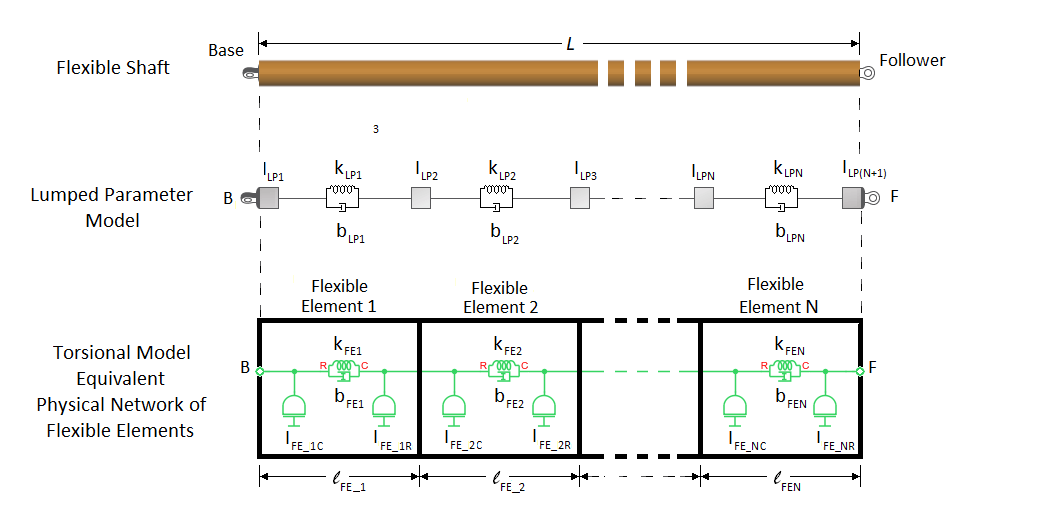
The block treats the shaft as an equivalent physical network of N flexible elements. Each flexible element, FEi, represents a short section of the driveshaft and contains:
One spring, kFE_i, for torsional compliance. The network has a total of N springs.
One damper, bFE_i, for material damping. The network has a total of N dampers.
Two inertias, IFE_iC and IFE_iR, for rotational resistance. The inertias of neighboring flexible elements are consolidated together so that the network has a total of inertias.
For an axially homogeneous shaft, the flexible element lengths, compliance, damping, and distributed inertias in the physical network are equal, such that:
For an axially inhomogeneous shaft, the amount of compliance, damping, and R-node and C-node inertia can differ for individual flexible elements in the physical network model.
The balance between model fidelity and simulation speed depends on N, the number of flexible elements that the block uses to represent the shaft. For information on balancing simulation speed and model fidelity, see Improve Simulation Speed or Accuracy.
The block allows you to specify a minimum number of flexible elements, Nmin, as the value for the Minimum number of flexible elements parameter. However, the number of flexible elements that the block actually uses depends on the complexity of the shaft that it is modeling. If the block requires more flexible elements than you specify to solve a model that contains axial inhomogeneity, intermediate supports, concentric disks or masses, static unbalances or external forces, then .
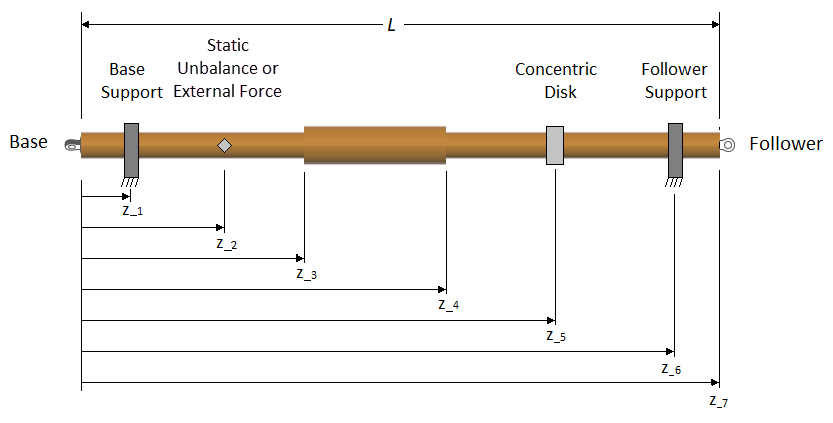
For example, suppose that, for the complex shaft in the diagram, you specify
axial locations for the supports, static unbalance or external force, larger
diameter section, and concentric disk. You set the parameter for
Nmin to 7.
If model bending is on, the torsion model flexible element locations account for the locations of static unbalances or external forces and concentric rigid masses, so that the torsion flexible elements align with the bending flexible elements. During simulation, the torsion model is independent of any static unbalances, external forces, or concentric rigid masses.
The algorithm for the block determines the number of flexible elements and the length of the individual elements that are required to solve the simulation:
The block places one node at the base and follower ends of the shaft. These nodes are considered fixed in axial location because they represent physical entities along the shaft axis. In the diagram, fixed nodes are shown in red. The block evenly distributes the other five (Nmin-2) internal nodes along the length of the shaft. It then places a flexible element between each consecutive pair of nodes.
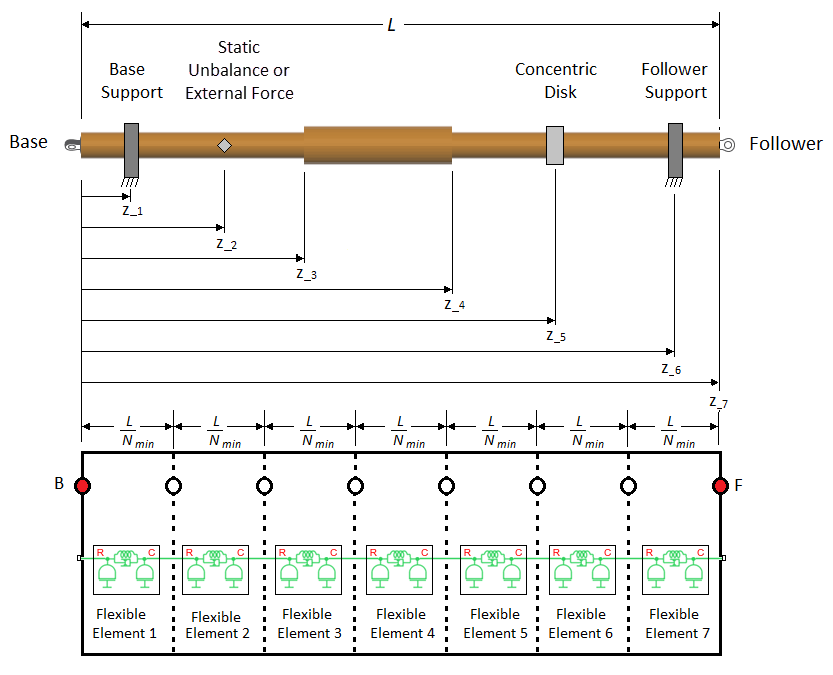
For an end-supported, axially homogenous shaft, with no static unbalances, external forces, or attached concentric disks, depending on the other parameter options and values that you specify, the block might be able to solve the simulation using only Nmin flexible elements of equivalent lengths:
In most cases, however, the block can only solve the simulation if it adds more flexible elements.
To add more flexible elements, the block places fixed internal nodes at these locations:
Each shaft support location. The block allows you to specify the number and location of shaft supports. For the shaft in the diagram, there are supports at z1 and z6.
Each static unbalance or external force. For the shaft in the diagram, there is a static unbalance at z2.
Each rigid mass. Rigid masses are concentrically attached disks or point masses. For the shaft in the diagram, there is a rigid mass, represented as a disk, at z5.
Each parameterization segment boundary. Parameterization boundaries are locations along an axially inhomogeneous shaft where two neighboring sections of the shaft vary in stiffness, inertia, or geometry. The block allows you to define the parameterization segment boundary locations. For the shaft in the diagram, there are segment boundaries at z3 and z4.
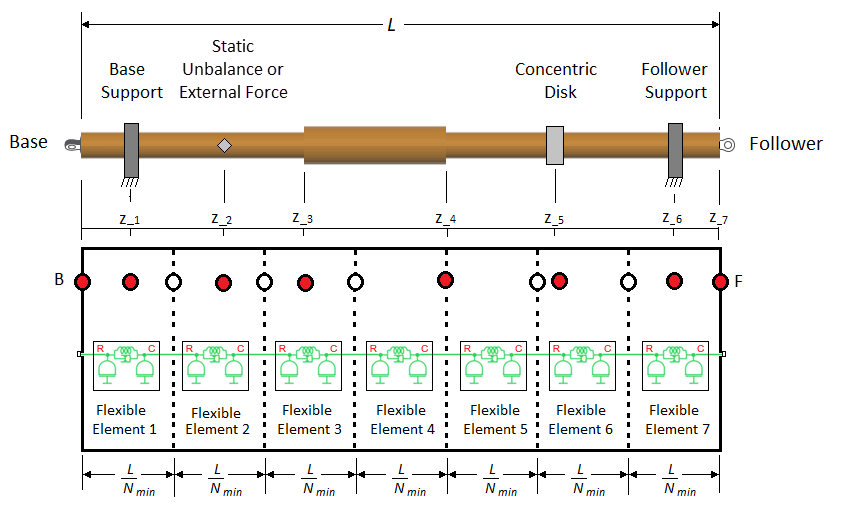
Note that the block did not add a node at z4 because a node was already added in the previous step of the algorithm. However, the node is now fixed because it represents a physical entity along the shaft length.
The block adjusts the nonfixed node locations between the fixed nodes so that they are evenly distributed.
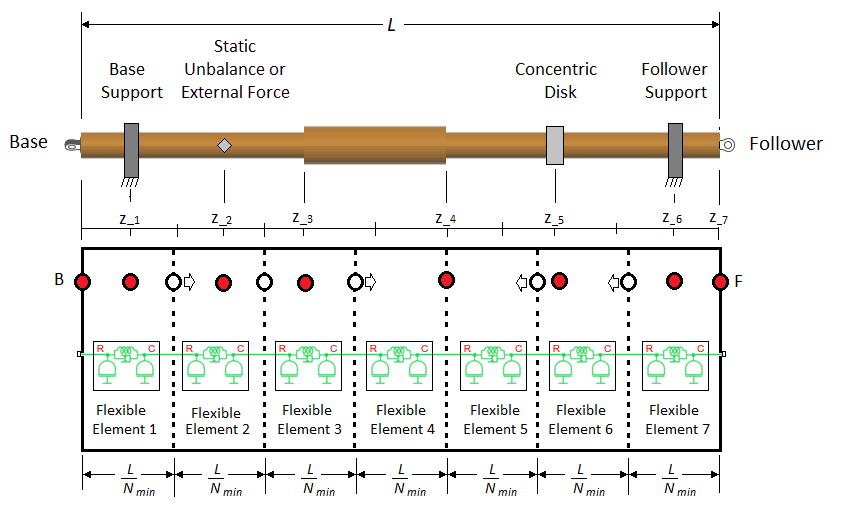
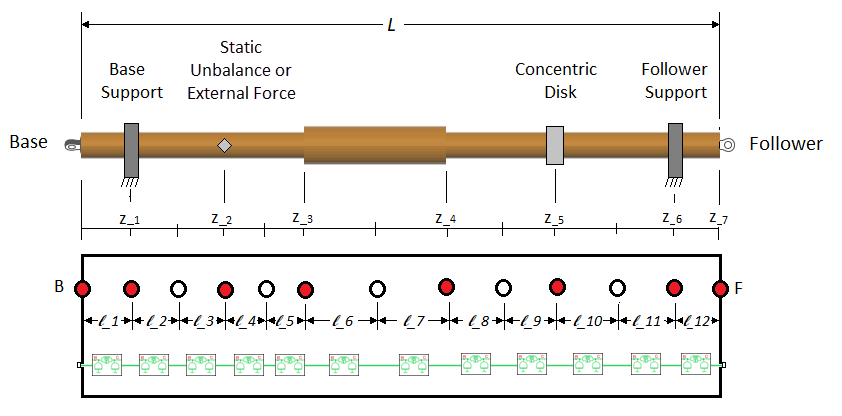
Finally, the block places flexible elements between each node. The length of each flexible element corresponds to the center-to-center distances between the neighboring nodes. The block distributes the inertia among the flexible elements based on the length of the individual element and the corresponding shaft geometry. Ultimately, this complex shaft is represented by 12 flexible elements, with , , , , , , and .
If Nmin is large enough to yield a number of unfixed nodes that is greater than the number of fixed nodes, the block distributes more than one unfixed node between each set of neighboring fixed nodes.
You can parameterize the torsion model by using either stiffness, k, and the polar moment of inertia, J, or the dimensions and material properties of the shaft.
The stiffness and inertia for each element are computed from the shaft dimensions and material properties as:
where:
JP is the polar moment of inertia of the shaft at the flexible element location.
D is the outer diameter of the shaft at the flexible element location.
d is the inner diameter of the shaft at the flexible element location. For a solid shaft, . For an annular shaft, .
is the flexible element length.
m is the mass of the shaft at the flexible element location.
J is the moment of inertia of the shaft at the flexible element location.
ρ is the density of the shaft material.
G is the shear modulus of elasticity of the shaft material.
k is the rotational stiffness of the flexible element.
For either torsional parameterization, the internal material damping is defined by the damping ratio, c, for a single-flexible element model with the equivalent torsional stiffness and inertia. The damping coefficient is then , where the undamped natural frequency is The damping torque applied across an individual flexible element of a lumped mass model is equivalent to the product of the damping coefficient and the relative rotational velocity of that flexible element.
Bending Models
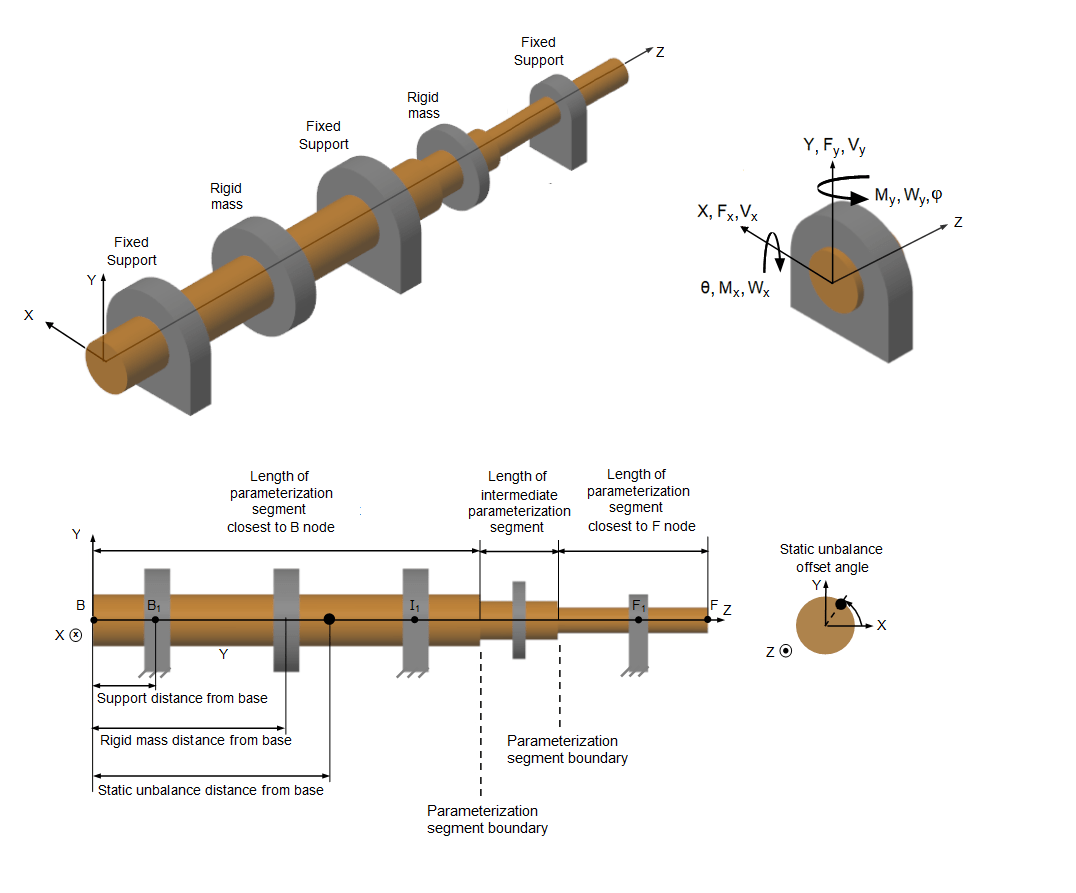
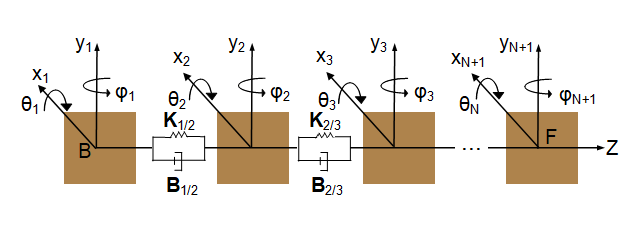
The Shaft Geometry, Support Loading, and Motion figure shows how to measure:
The static unbalance offset angle, which is the angle of a static unbalance about the shaft axis relative to the x axis
The distances of a support, a rigid mass, and a static unbalance, relative to the base end of the shaft, B
The parameterization of the segment lengths
In the figure, the shaft has three fixed supports:
B1 — Base end support
I1 — Intermediate support
F1 — Follower end support
The shaft has translational velocity V, rotational velocity W, and exerts forces F, and moments M, on the supports. The curved arrows and sign conventions follow the right-hand rule. The signs of the physical signals that the block outputs correspond to the arrows that represent the forces, moments, and velocities of the shaft acting on the supports.
The vector signals are:
Force,
Moment,
Translational velocity,
Rotational velocity,
If the shaft has two supports, each vector signal has a length of four. Force, for example, is then .
If the shaft has four supports, each vector signal has a length of eight. Force, for example, is then .
Shaft Geometry, Support Loading, and Motion
Like the torsion model, the lumped mass method for the bending model discretizes the distributed, continuous properties of the shaft into a finite number, N, of flexible elements. The N flexible elements correspond to lumped inertias connected in series by damping and spring elements. However, for the bending model, each mass has four degrees of freedom: translation and rotation in both the x and y directions perpendicular to the shaft axis.
The lumped mass equation of motion [1] is
where:
M is the matrix that represents the mass of the shaft.
B is the matrix for the internal damping and support damping.
GDisk is the matrix that accounts for disk gyroscopics
Ω is the shaft torsional velocity during simulation.
K is the matrix for the spring stiffness.
is the vector that represents the degrees of freedom for all nodes.
is the vector that represents external forces due to the application of static mass unbalance.
The equation for the mass matrix [5] is
where:
is the mass matrix for an individual flexible element. For each flexible element, half of the mass and moment of inertia is transferred to the nodes at both ends of the flexible element. The matrix has nonzero elements in the rows and the columns:
where:
is the flexible element length along the shaft between internal nodes. To determine the length of each flexible element, the block uses the algorithm that is described in Node Placement Algorithm. Each flexible element contains two inertias. Each inertia has two translational degrees of freedom, two rotational degrees of freedom, and one stiffness matrix.
Each flexible element in the equivalent physical model for bending in the XZ-plane (the beam translation in the X-direction and rotation about the Y-axis) and in the physical model for bending in the YZ-plane (the beam translation in the Y-direction and rotation about the X-axis) then contains two masses, two inertias, and a stiffness matrix.
To determine the internal node locations, and therefore the number and lengths of the flexible elements, the block uses the same node-placement algorithm as it uses for the torsion model. For more information, see Node Placement Algorithm.
m is the flexible element mass. m depends on the outer, D, and inner, d, diameters, the density, ρ, of the shaft and the length of the flexible element, such that .
Id, the half-element mass moment of inertia about an axis perpendicular to the shaft axis, depends on the mass, m, length, , and torsion moment of inertia, J, of the flexible element, such that .
is the summed mass matrices of the rigid masses concentrically attached to the shaft.
The mass properties of each rigid mass that is concentrically attached to the shaft are added to the closest node, , such that
where ID,disk,i is the mass diametric moment of inertia about an axis perpendicular to the shaft for a rigid disk attached to the ith node. The model assumes that the disk is thin, so the shaft can still bend on either side of the axial location with the disk. A concentric point mass has .
The equation for the damping matrix is
where:
α is the damping constant proportional to mass.
β is the damping constant proportional to stiffness.
Bsupport is the damping coefficient at each support. For a support at the ith node, the damping matrix, in terms of global coordinates, is
where:
is the support translational damping.
is the support rotational damping.
accounts for the gyroscopic effects of any concentrically attached disks, and is defined as
where IP,disk,i is the mass polar moment of inertia about the shaft axis for the disk attached to the ith node. The mass polar moment of inertia for a concentric point mass is .
The equation for the bearing stiffness matrix is
where:
is the stiffness matrix for an individual shaft flexible element. The stiffness matrix for the shaft flexible element, between the ith and the nodes, has nonzero elements in the rows and the columns, such that
where:
is the flexible element length.
EI is the shaft rigidity.
Ksupport is the stiffness at each support. For a support at the ith node, the stiffness matrix, in terms of global coordinates, is
where:
is the support translational stiffness.
is the support rotational stiffness.
The support stiffness matrix,
Ksupport, is nonzero only if you
select Bearing matrix or Speed-dependent
bearing matrix for the support. If you select the
Clamped mounting type, the kinematic conditions
of zero rotation and translation are applied to the degrees of freedom that
correspond to the support node (B1, I1,
I2, or F1). If you select the
Pinned mounting type, the kinematic conditions of
zero translation are applied to the translational degrees of freedom that
correspond to the support node (B1, I1,
I2, or F1).
The table includes the boundary conditions applied to the lumped mass nodes with supports.
| Support Type | Boundary Condition for the Lumped Mass Equation |
|---|---|
Clamped | |
Pinned | |
Bearing Matrix | Ksupport is nontrivial. |
Speed-dependent bearing
matrix | Ksupport is nontrivial and depends on shaft rotation speed. At each time step, KSupport is calculated as: where:
|
The matrix that represents the degrees of freedom for all nodes, , is calculated such that the degrees of freedom for the ith and the nodes are
External forces due to each static mass unbalance are applied to the closest node. The forcing at the node is
where:
mεj is the jthstatic unbalance, located at the ithnode.
Ωi is the shaft rotational velocity during simulation for the ith node.
φshaft, i is the torsion lumped mass rotation angle for the ith node.
When the block models an external force that excites the shaft at a multiple or fraction of the rotation speed:
where:
Fmag,j is the jth element of the External force magnitudes vector parameter.
p is the jth element of the External force frequency harmonic of rotor speed vector parameter.
ϕfoffset is the jth element of the External force offset angles vector parameter.
The node index i is the node at the z-axial position of the force.
For the eigenmodes method, the block reduces the bending dynamics from the degrees of freedom that the bending model lumped mass method provides, to M degrees of freedom, where M is the number of modes.
The block computes the bending mode properties of the shaft during model compilation, then solves the modal mass-spring-damper systems during model simulation.
Reducing the degrees of freedom in the model dynamics and separating the calculations into compile-time and run-time tasks improves simulation performance. The eigenmodes method assumes the mode shapes are unaffected by damping. Therefore, the method is best suited to models that include limited disk gyroscopic and support damping.
During compilation, the block computes the approximate damped eigenmodes using these steps:
The block computes the matrices using the same lumped mass equation of motion that it uses for the bending model lumped mass method:
For more information, see Bending Model Lumped Mass Method.
When determining the node axial locations for , the block uses one of two variations of the Node Placement Algorithm that it uses for the torsion model and the bending model lumped mass method. The variation that the block uses depends on whether, in the Advanced Bending settings, the Bending mode determination parameter is set to
Simscape determinedor toUser defined.If the Bending mode determination parameter is set to
Simscape determined, instead of using the Minimum number of flexible elements parameter for Nmin, as the lumped mass methods do, the eigenmodes method calculates Nmin aswhere:
L is the specified value of the Shaft length parameter.
dz is the specified value of the Shaft length increments for mode shape computations parameter.
To compute the m undamped eigenmodes and eigenfrequencies, the block uses the
eigsfunction. The equation takes the form :where:[HRight, λ] = eigs( sparse(K), sparse(M), mMax, 'smallestabs’ ) [HLeft, λ] = eigs( sparse(K), sparse(M), mMax, 'smallestabs’ )
HRightis the right eigenvector matrix. Each column is a right eigenmode in the coordinates.HLeftis the left eigenvector matrix. Each column is a left eigenmode in the coordinates.λrepresents the eigenvalues, which are the squares of the eigenfrequencies.mMax is the Limit number of modes parameter.
The number of eigenmodes computed, m, is less than mMax if:
There are modes with eigenfrequencies that exceed the specified value for the Eigenfrequency upper limit parameter. The block discards these modes.
The eigenvalues fail to converge. For more information, see
eigs.
If you set Bending mode determination to
User defined, the block computes the eigenvector matrix H for these parameters:X-direction mode shapes
Y-direction mode shapes
Shaft position
To determines the node axial locations for , the block uses the elements specified for the Shaft position parameter as the primary nodes.
To compute the modal rotation, θ and φ, for each node, the block uses the
gradientfunction. The equations take the form:θ = -gradient(Y direction mode shapes) φ = gradient(X direction mode shapes)
The block assembles the values from the X-direction mode shapes parameter, Y-direction mode shapes parameter, and modal rotations, θ and φ, into coordinates for each column of HLeft and HRight.
The block computes the modal matrices, MModal, KModal, BModal, GModal, and fModal, as:
Although the block computes undamped eigenmodes, H, in step 1, the modal damping matrix, BModal, and modal gyroscopics matrix, GModal, may model light damping. The block normalizes the matrices so that MModal is the identity matrix.
During simulation, the block simulates the eigenmode equation of motion:
where the modal degrees of freedom, , relate to the node degrees of freedom by:
Speed-Dependent Eigenmodes Method
The support stiffness and support damping vary if, in the
Supports settings, the mounting type parameter for any
of the supports is set to Speed-dependent bearing
matrix. The speed-dependent eigenmodes model accounts for
these effects by varying the modal properties,
HRight and
HLeft, BModal,
GModal, KModal, and
fModal as the shaft speed
changes. MModal is normalized to the
identity matrix for all shaft speeds, so it does not depend on shaft
speed.
If the shaft has speed-dependent bearing supports, then the block repeats the bending mode eigenmodes method steps for each element in the shaft speed vector. The shaft vector elements are the specified values, in the Supports settings, for the Bearing speed [s1,...,sS] parameter. During simulation, the modal stiffness, damping, and forcing magnitude are adjusted based on lookup tables of the properties versus the shaft speed.
That is, the block simulates the eigenmode equation of motion as:
where KModal, BModal, and fModal have the form:
where:
ΩRef is the specified value, in the Supports settings, for the Bearing speed [s1,...,sS] parameter.
KModal,Ref is the table of modal stiffnesses at each ΩRef.
BModal,Ref is the table of support damping at each ΩRef.
GModal,Ref is the table of disk gyroscopic damping at each ΩRef.
fModal,Ref is the table of modal forcing at each ΩRef.
The block correlates the mode shape similarity at different values of ΩRef and reorders modes, if necessary, so that each modal degree of freedom, , has properties that gradually change with the shaft speed.
Improve Simulation Speed or Accuracy
The balance between simulation accuracy and performance depends on N, the number of flexible elements that the block uses to represent the shaft. Simulation accuracy is a measure of how much the simulation results agree with mathematical and empirical models. Generally, as N increases, so does model fidelity and simulation accuracy. However, the computational cost of the simulation is also correlated to N, and as computational cost increases, performance decreases. Conversely, as N decreases, simulation speed increases but simulation accuracy decreases.
To increase simulation accuracy for the lumped mass method for either a torsion or bending model, increase the minimum number of flexible elements, Nmin. The single-flexible-element torsion model exhibits a torsional eigenfrequency that is close to the first eigenfrequency of the continuous, distributed parameter model. For greater accuracy you can select 2, 4, 8, or more flexible elements. For example, the four lowest torsional eigenfrequencies are represented with an accuracy of 0.1, 1.9, 1.6, and 5.3 percent, respectively, by a 16-flexible-element model.
To increase simulation accuracy for the eigenmodes method to a bending model:
If simulating with static eigenmode dependency on rotation speed, verify that the Nominal shaft speed for bending modes parameter is close to the simulation shaft speed. This parameter may affect model results if you parameterize a rigid disk attached to the shaft with a large mass moment of inertia about the shaft axis or specify any speed-dependent bearing matrix supports.
If simulating with dynamic eigenmode dependency on rotation speed, verify that, in the Supports settings, the specified values for the Bearing speed [s1,...,sS] span the shaft speed range of the simulation or that saturation of the support stiffness and damping at shaft speeds outside the range is an acceptable approximation.
In the Advanced Bending settings, decrease the value of the Shaft length increments for mode shape computations parameter. Reducing the value can increase the accuracy of modal frequencies and shapes.
Decrease the support damping and disk polar moment of inertia about the shaft axis. Simscape™ computations of the mode shapes and frequencies before simulation do not account for this damping.
Check the sensitivity to the Advanced Bending settings by using your parameters in the flexible shaft model in the Shaft with Torsional and Transverse Flexibility example. Adjust the parameters and use the links provided in the example to examine how the values affect the eigenmode frequencies and shapes. Adjust the parameter values in your model accordingly.
Increase the values of the Eigenfrequency upper limit and Limit number of modes parameters. The highest modal frequency in the simulation must be significantly larger than the shaft rotation frequency.
Assumptions and Limitations
The distributed parameter model of a continuous torsional shaft is approximated by a finite number, N, of lumped masses.
Shaft rotation and torsion flexibility excite shaft bending, but bending does not affect shaft rotation and torsion flexibility.
Rigid point masses or disks attached to the shaft have thin lengths parallel to the shaft axis.
For the eigenmodes bending model, damping does not affect the eigenfrequencies.
Shaft bending is not transmitted between Flexible Shaft blocks.
Relative to the shaft length, the shaft outer diameter is small.
Relative to the shaft length, the bending deflection is small.
Static mass unbalances are the only shaft-bending external exciting loads.
Shaft supports are stationary.
Gyroscopic effects of the rigid disks are considered; gyroscopic effects of the shaft itself are neglected.
Static mass unbalance forcing in the eigenmodes method uses the rotation speed at the shaft midpoint.
If the shaft models torsion only and uses the parameterization options By stiffness and inertia or By segment stiffness and inertia, the block uses only two supports, one each at the B and F ends.
Ports
Output
Conserving
Parameters
References
[1] Adams, M.L. Rotating Machinery Vibration. CRC Press, NY: 2010.
[2] Bathe, K. J. Finite Element Procedures. Prentice Hall, 1996.
[3] Chudnovsky, V., D. Kennedy, A. Mukherjee, and J. Wendlandt. Modeling Flexible Bodies in SimMechanics and Simulink. MATLAB Digest, Volume 14, Number 3. May 2006.
[4] Kane and Torby, “The Extended Modal Reduction Method Applied to Rotor Dynamic Problems,” Journal of Vibration and Acoustics 113, no. 1 (January 1, 1991): 79–84. https://doi.org/10.1115/1.2930159.
[5] Miller, S., T. Soares, Y. Van Weddingen, J. Wendlandt. Modeling Flexible Bodies with Simscape Multibody. The MathWorks, 2017.
[6] Muszynska, A. Rotordynamics. Taylor & Francis, 2005
[7] Rao, S.S. Vibration of Continuous Systems. Hoboken, NJ: John Wiley & Sons, 2007.