このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
プログラムによる近似
多項式モデルのための MATLAB 関数
2 つの MATLAB® 関数が、多項式モデルを用いてデータをモデリングできます。
多項式近似関数
物理的な状況のモデリングを試みる場合、現在の状況において特定次数のモデルが有意義であるかについて考察することは常に重要です。
非多項式項をもつ線形モデル
この例では、非多項式項を含む線形モデルによって、データに当てはめる方法を示します。
多項式関数がデータに対して十分なモデルを与えない場合、非多項式項をもつ線形モデルを使用して試すことができます。たとえば、パラメーター 、、 に関しては線形で、 のデータに関しては非線形であるような、次の関数を考えます。
連立方程式を作成して解き、パラメーターを求めることによって、未知の係数 、、 を計算できます。次の構文では、"計画行列" を作成することでこれを行います。ここで、各列は応答 (モデルの項) の予測に使用する変数を表し、各行はそれらの変数の 1 つの観測に対応します。
t と y を列ベクトルとして入力します。
t = [0 0.3 0.8 1.1 1.6 2.3]'; y = [0.6 0.67 1.01 1.35 1.47 1.25]';
計画行列を作成します。
X = [ones(size(t)) exp(-t) t.*exp(-t)];
モデルの係数を計算します。
a = X\y
a = 3×1
1.3983
-0.8860
0.3085
したがって、データのモデルは次のように与えられます。
次に、等間隔の点においてモデルを計算し、元のデータとモデルをプロットします。
T = (0:0.1:2.5)'; Y = [ones(size(T)) exp(-T) T.*exp(-T)]*a; plot(T,Y,'-',t,y,'o'), grid on title('Plot of Model and Original Data')
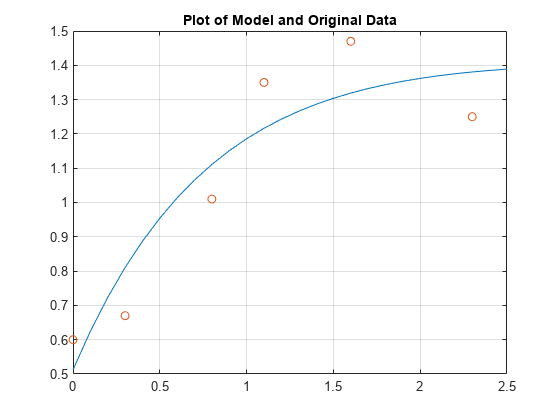
重回帰
この例では、複数の予測子変数が含まれる関数のモデル データに重回帰を使用する方法を示します。
y が複数の予測子変数を含む関数の場合、変数の関係を表す行列方程式を、データの追加に合わせて拡張しなければなりません。これは、"重回帰" と呼ばれます。
と のいくつかの値に対して量 を測定します。これらの値を、ベクトル x1、x2、y にそれぞれ格納します。
x1 = [.2 .5 .6 .8 1.0 1.1]'; x2 = [.1 .3 .4 .9 1.1 1.4]'; y = [.17 .26 .28 .23 .27 .24]';
データの多変量モデルを、次のように考えます。
重回帰によって、未知の係数 、、 は、モデルからのデータの偏差の二乗和を最小化することで求められます (最小二乗近似)。
計画行列 X を形成することによって、連立方程式を作成して解きます。
X = [ones(size(x1)) x1 x2];
バックスラッシュ演算子を使用してパラメーターを求めます。
a = X\y
a = 3×1
0.1018
0.4844
-0.2847
データの最小二乗近似モデルは、次のようになります。
モデルを検証するために、モデルから求めた点と観測データ点との偏差の絶対値から最大値を求めます。
Y = X*a; MaxErr = max(abs(Y - y))
MaxErr = 0.0038
この値がデータ値に比べて十分小さいので、データへの近似がうまくいっているモデルであることを確信できます。
プログラムによる近似
この例では、MATLAB 関数を用いて以下の操作を行う方法を示します。
相関係数の計算
例では、ここで、統計的な相関を決め、データのモデリングが適切であるか確かめるために、変数 cdate と pop を決定します。相関係数の詳細は、線形相関を参照してください。
データへの多項式近似
信頼限界のプロットと計算
信頼限界は、予測された応答に対する信頼区間です。区間の幅は、近似がどの程度正確であるかを示します。
この例では、サンプル データ census に polyfit と polyval を適用し、2 次多項式モデルの信頼限界を求めます。
次のコードでは、 の区間を使用します。これは、大規模な標本に対する 95% 信頼区間に相当します。
95% の区間は、新しい観測が区間内に入る可能性が 95% であることを示します。
