対話型の近似
基本的な近似 UI
MATLAB® の基本的な近似 UI は、対話的に以下を行うことができます。
スプライン内挿、形状維持内挿、または 多項式 (最高 10 次) を使用したデータ モデリング
1 つ以上の近似をデータと共にプロット
近似の残差をプロット
モデルの係数を計算
残差のノルム (モデルのデータへの近似の程度分析に使用可能な統計) を計算
モデルを使用した内挿またはデータ範囲外での外挿
ダイアログ ボックス外で使用するため、係数と計算結果の値を MATLAB ワークスペースに保存
新しいデータによる近似再計算およびプロット再作成用に MATLAB コードを生成
メモ
基本的な近似 UI は 2 次元プロットにのみ利用可能です。より高度な近似および回帰分析の詳細については、Curve Fitting Toolbox™ ドキュメンテーションと Statistics and Machine Learning Toolbox™ ドキュメンテーションを参照してください。
基本的な近似のための準備
基本的な近似 UI では、近似前にデータを昇順で並べ替えます。データ セットが大きく、値が昇順に並べ替えられていない場合、近似前の、基本的な近似 UI によるデータの前処理に時間がかかります。
先にデータを並べ替えることで基本的な近似 UI を高速化できます。データ ベクトル x と y から、並べ替えられたベクトル x_sorted と y_sorted を作成するには、MATLAB 関数 sort を使用します。
[x_sorted, i] = sort(x); y_sorted = y(i);
基本的な近似 UI の開始
基本的な近似 UI を利用するには、まず x と y データ (のみ) を生成する MATLAB プロット コマンドを用いて Figure ウィンドウにデータをプロットしなければなりません。
基本的な近似 UI を開くには、Figure ウィンドウの上部から [ツール]、[基本的な近似] を選択します。
例: 基本的な近似 UI の使用
この例では基本的な近似 UI を使用して多項式回帰の近似、可視化、解析、保存およびコード生成を行う方法を説明します。
人口調査データの読み込みとプロット
ファイル census.mat は、1790 年から 1990 年までの 10 年間隔の米国での人口のデータを含みます。
データを読み込みプロットするためには、MATLAB プロンプトで次のコマンドを入力します。
load census plot(cdate,pop,'ro')
load コマンドは、MATLAB ワークスペースに次の変数を追加します。
cdate: 1790 年から 1990 年までの 10年ごとの年度を示す列ベクトルです。これは、予測変数です。pop:cdateの中の各年度に対応する米国の人口が記された列ベクトルです。これは、応答変数です。
データ ベクトルは、年度によって昇順に並べ替えられます。プロットは、人口を年度の関数として表します。
これで、経時的な人口増加をモデル化する式に、データを近似する準備ができました。
3 次多項近似による人口調査データの予測
Figure ウィンドウで、[ツール]、[基本的な近似]を選択することにより、[基本的な近似] ダイアログ ボックスを開きます。
[基本的な近似] ダイアログ ボックスの [近似タイプ] エリアで、[3 次多項式] チェック ボックスを選択してデータを 3 次多項式で近似します。
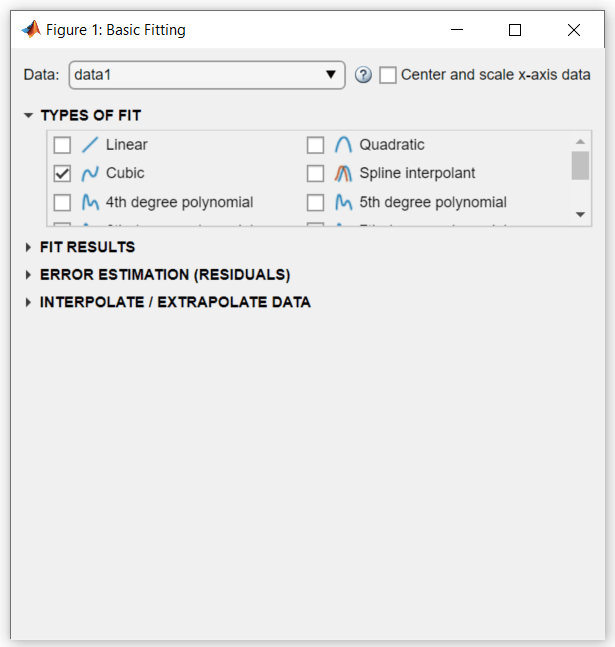
MATLAB は、選択に従ってデータを近似し、次のように 3 次回帰線をグラフに追加します。
近似の計算中に、MATLAB で問題が発生し、次の警告が表示されます。
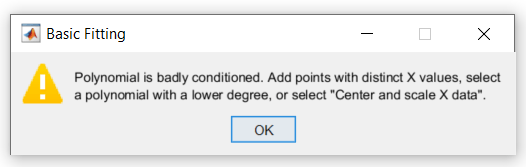
この警告は、モデルに対して計算された係数が応答 (測定された人口) におけるランダムなエラーに影響されることを示します。これは、さらに良い近似を得るための提案でもあります。
引き続き、3 次近似を使用します。人口調査データに新しい観測を追加することはできないので、値を "z スコア" に変換してから近似を再計算することで、近似を向上させます。ダイアログ ボックスの右上の [x 軸データのセンタリングとスケーリング] チェック ボックスをオンにして、基本的な近似ツールに変換を実行させます。
データのセンタリングとスケーリングの動作方法については、基本的な近似ツールが近似を計算する方法についてを参照してください。
[誤差推定 (残差)] で、[残差ノルム] のチェック ボックスを選択します。[プロット スタイル] で [棒グラフ] を選択します。
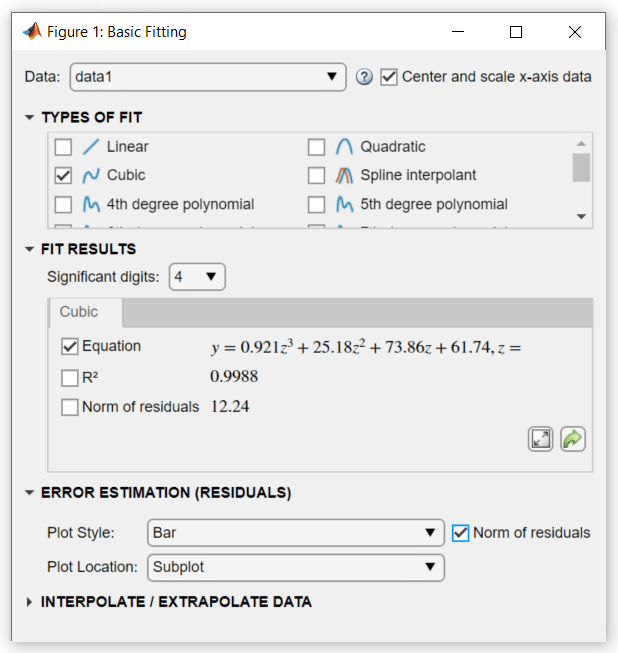
これらのオプションを選択すると、残差のサブプロットが棒グラフとして作成されます。
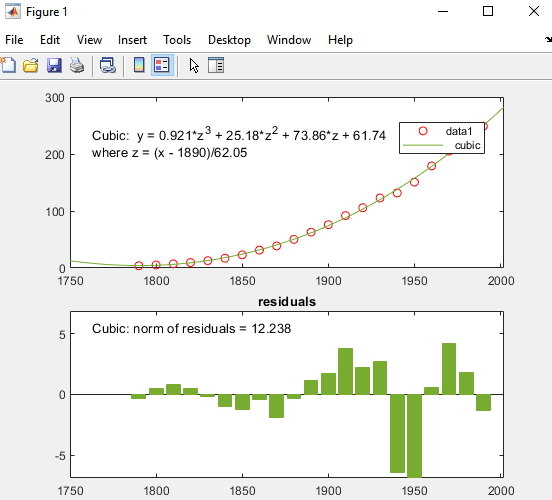
人口が減少していることを示す 1790 年以前には、3 次式の予測は良くありません。1790 年以降は、モデルがデータを良く近似するように見えますが、残差のパターンは、モデルが正規誤差の仮定を満たさないことを示します。これは、最小二乗近似の基本です。凡例で識別された [data 1] ラインは、観測された x (cdate) および y (pop) データ値です。[3 次多項式] 回帰線はデータ値のセンタリングとスケーリング後の近似を表します。ツールで変換された z スコアを使用して近似が計算される場合も、この数字は元のデータ単位を示すことに注意してください。
比較のため、[近似タイプ] エリアで他の多項式を選択して人口調査データに他の式の近似を試みてください。
3 次近似パラメーターの表示と保存
[基本的な近似] ダイアログ ボックスで [結果を展開] ボタン  をクリックすると、係数の推定値と残差ノルムが表示されます。
をクリックすると、係数の推定値と残差ノルムが表示されます。
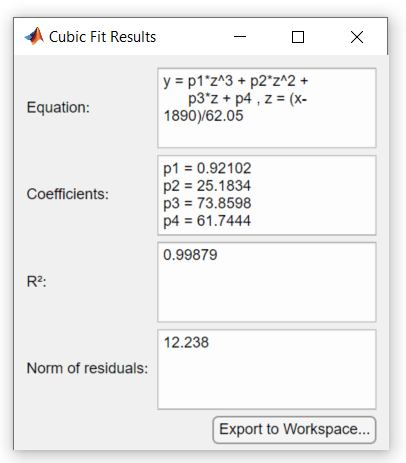
[数値結果] パネルの [ワークスペースにエクスポート] ボタンをクリックすることにより、近似のデータを MATLAB ワークスペースへ保存します。[近似をワークスペースに保存] ダイアログ ボックスが開きます。
すべてのチェック ボックスをオンにし、[OK] をクリックして、近似パラメーターを MATLAB 構造体の fit として保存します。
fit
fit =
struct with fields:
type: 'polynomial degree 3'
coeff: [0.9210 25.1834 73.8598 61.7444]これで、基本的な近似 UI の外部で、MATLAB プログラミングにおいて近似の結果を使用できます。
決定係数 R2
決定係数、つまり R の二乗 (R2 と表記) を計算することによって、多項式回帰により観測されたデータがどれくらい正確に予測されるかを表示できます。0 ~ 1 までの R2 統計は、独立変数が従属変数の値の予測にどれくらい役に立つかを測定します。
R2 値が 0 に近い場合、近似がモデル
y = constantと同程度であることを示します。R2 値が 1 に近い場合、独立変数が従属変数のほとんどの変化量を説明することを示します。
R2 は、観測された従属値とその値に対して近似で予測される値との符号付きの差異である、"残差" から計算されます。
| residuals = yobserved - yfitted | (1) |
この例の 3 次近似の R2 の数値、0.9988 は、[基本的な近似] ダイアログ ボックスの [近似の結果] にあります。
3 次近似の R2 の数値を線形最小二乗近似と比較するには、[近似タイプ] で [線形] を選択し、R2 の数値、0.921 を取得します。この結果は、人口データの線形最小二乗近似で分散の 92.1% が説明されることを示します。このデータの 3 次近似によってこの分散の 99.9% が説明されるので、後者の方が優れた予測子のように思われます。しかし、3 次近似は 3 つの変数 (x、x2、および x3) を使用して予測するため、基本 R2 値はこの近似がどれくらいロバストな近似かということが完全には反映されません。多変量の適合度をより適切に評価する尺度は、調整された R2 です。調整された R2 の計算方法と使い方の詳細は、近似の残差と適合度を参照してください。
人口値の内挿と外挿
1965 年 (元のデータにはない日付) の米国の人口を内挿するために、3 次モデルを利用するものとします。
[基本的な近似] ダイアログ ボックスの [データの内挿/外挿] で、[X] の値 1965 を入力し、[評価データのプロット] ボックスをオンにします。
メモ
スケーリングとセンタリングを行っていない X の値を使用します。3 次多項近似による人口調査データの予測で係数を取得するために X の値をスケーリングするように選択した場合でも、それを最初にセンタリングしたりスケーリングする必要はありません。基本的な近似ツールは、ユーザーから直接的には分かりませんが必要な調整を行います。
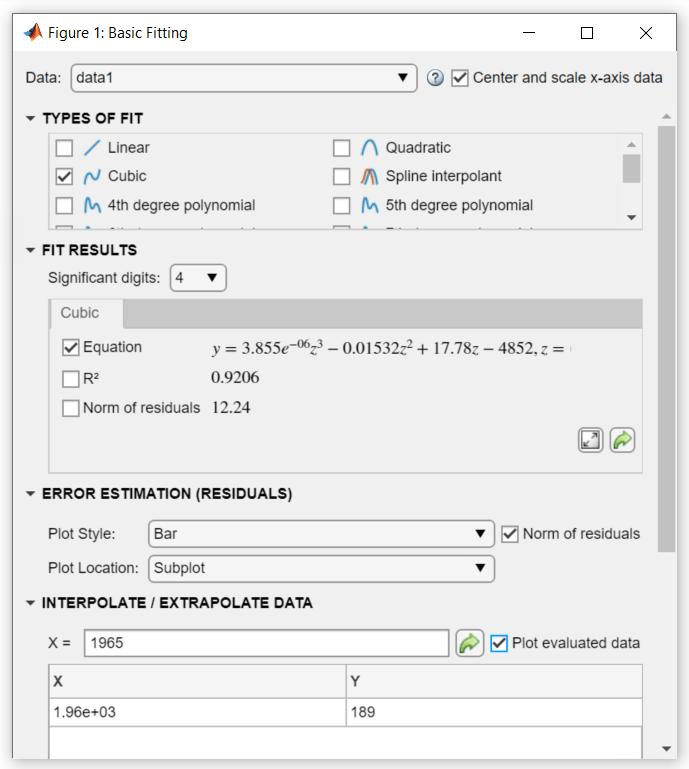
X の値と f(X) に対応する値は、下記のように近似から計算され、プロットされます。
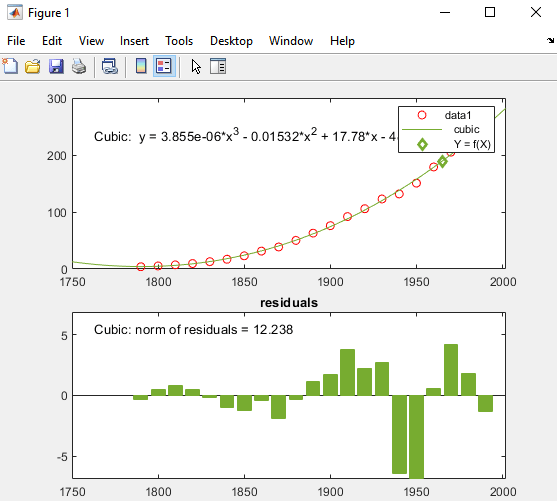
結果を再現するコード ファイルの生成
基本的な近似セッションの終了後、新しいデータを使用して近似の計算とプロットの作成を再度行うための MATLAB コードを生成できます。
Figure ウィンドウで、[ファイル]、[コードの生成] を選択します。
これにより、関数が作成され、MATLAB エディターに表示されます。このコードは、[基本的な近似] ダイアログ ボックスで対話的に行ったことをプログラムで再現する方法を示します。
最初の行の関数名を
createfigureから、censusplotのように、わかりやすい名前に変更します。このコード ファイルをcensusplot.mというファイル名で現在のフォルダーに保存します。この関数の最初の行は次のとおりにします。function censusplot(X1, Y1, valuesToEvaluate1)
ランダムに摂動する新しい census データを生成します。
rng('default') randpop = pop + 10*randn(size(pop));新しいデータと再計算した近似を用いてプロットを作成し直します。
censusplot(cdate,randpop,1965)
元のグラフにプロットされた x,y 値 (
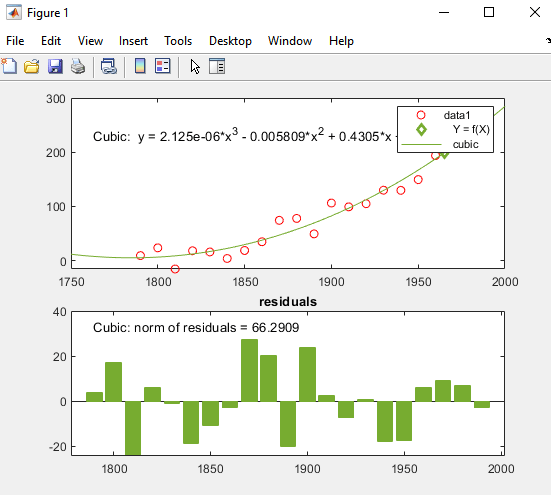
data 1) に加え、マーカーの x 値の 3 つの入力引数が必要です。次の図は、生成されたコードが作成したプロットを示します。新しいプロットは、y データ値、3 次多項式近似式、および棒グラフの残差値を除き、コードを生成するのに使用した図の表示と予想どおりに一致します。
基本的な近似ツールが近似を計算する方法について
基本的な近似ツールは、関数 polyfit を呼び出して多項式近似を計算します。関数 polyval を呼び出して、近似を評価します。polyfit は、与えられた入力を解析し、データが指定された次数で近似できる条件を備えているかを決定します。
悪条件のデータが見つかると、polyfit はできるだけ適切に回帰を計算しますが、近似を向上させる可能性についての警告も返します。基本的な近似の例のセクション3 次多項近似による人口調査データの予測にこの警告が表示されています。
モデルの信頼性を向上させる方法の 1 つは、データ点を追加することです。ただし、いつでもデータ セットに観測を追加できるわけではありません。代わりに、予測子変数を変換して、センターとスケールを正規化する方法があります。(この例では、予測子は人口調査の日付のベクトルです)
関数 polyfit は、"z スコア" を計算して、正規化します。
ここで、x は予測データ、μ は x の平均、σ は x の標準偏差です。z スコアのデータは 0 の平均値と 1 の標準偏差をもちます。基本的な近似 UI では、[x 軸データのセンタリングとスケーリング] チェック ボックスをオンにして、予測子データを z スコアに変換します。
センタリングとスケーリングの後、y データに対してモデルの係数が z の関数として計算されます。これらは、x の関数として y に対して計算された係数とは異なり、さらにロバストです。モデルの形式と残差のノルムは変更されません。基本的な近似 UI は、近似が元の x データと同じスケールでプロットされるように z スコアを自動的にリスケーリングします。
センタリングとスケーリングされたデータが、最終プロットを作成する中間データとして使用される方法を理解するために、コマンド プロンプトで以下を入力します。
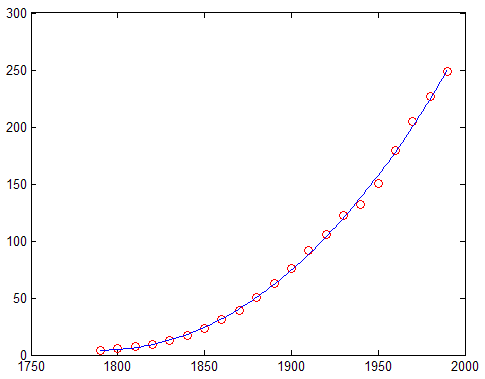
close load census x = cdate; y = pop; z = (x-mean(x))/std(x); % Compute z-scores of x data plot(x,y,'ro') % Plot data as red markers hold on % Prepare axes to accept new graph on top zfit = linspace(z(1),z(end),100); pz = polyfit(z,y,3); % Compute conditioned fit yfit = polyval(pz,zfit); xfit = linspace(x(1),x(end),100); plot(xfit,yfit,'b-') % Plot conditioned fit vs. x data
センタリングおよびスケーリングされた 3 次多項式プロットは、青線で表示しています。
コードでは、z の計算でデータを正規化する方法が説明されています。関数 polyfit は、呼び出すときに 3 つの戻り引数を指定すると、自動的に変換を実行します。
[p,S,mu] = polyfit(x,y,n)
p は、正規化された x に基づいています。返されるベクトル mu には、x の平均および標準偏差が含まれます。詳細は、polyfit のリファレンス ページを参照してください。