このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
非線形 Simulink モデルの記述関数の解析
この例では、飽和非線形性のモデルに対して、正弦波入力の記述関数解析を実行するために周波数応答推定を使用する方法を示します。
記述関数の解析は、非線形システムの周波数応答を調べるための手法です。これは、線形周波数応答解析の延長です。線形システムでは、伝達関数は、入力信号の周波数にのみ依存します。非線形システムでは、正弦波などの入力信号の特定のクラスを非線形要素に適用すると、記述関数を使用して非線形要素を表すことができます。記述関数は、入力周波数だけでなく、入力振幅にも依存します。記述関数の解析は、周波数応答の解析からリミット サイクルの予測まで、広範囲に適用されます。
記述関数解析の最も一般的なタイプである正弦波入力の記述関数解析を使用するには、モデルが次の条件を満たしていなければなりません。
非線形性が時不変である。
非線形性が、入力正弦波に応答して低調波を生成しない。
非線形性によって生じた超高調波をシステムが除去する (この条件は通常、フィルター処理仮説と呼ばれます)。
この例では、これらの条件を満たしている飽和非線形性のモデルに対して、記述関数の解析を実行します。
Simulink® モデルを開きます。
mdl = 'scdsaturationDF';
open_system(mdl)
飽和非線形性には、次のような正弦波入力の記述関数があります。
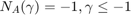
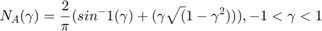
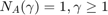
ここで、上限と下限がそれぞれ 0.5 と -0.5 の飽和に対し 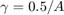 であり、A は正弦波入力信号の振幅です。
であり、A は正弦波入力信号の振幅です。
振幅が 0.1 ~ 2.1 で変化する場合、記述関数 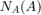 を計算してプロットします。この記述関数は
を計算してプロットします。この記述関数は saturationDF.m に実装されています。
A = linspace(0.1,2.1,21); N_A = saturationDF(0.5./A); plot(A, N_A) xlabel('Amplitude') ylabel('N_A(A)') title('Describing Function for Saturation')
5 rad/s の固定周波数の同じセットの振幅に対して frestimate を使用し、飽和非線形性の記述関数を計算できます。飽和の記述関数は、周波数に依存しないため、単一の周波数での解析は十分に実行できます。
入力と出力の線形解析ポイントを定義します。
io(1) = linio('scdsaturationDF/In1',1,'input'); io(2) = linio('scdsaturationDF/Saturation',1,'output');
振幅ごとに、5 rad/s の固定周波数と特定の振幅をもつ sinestream の入力を作成します。次に、この入力信号を使用して frestimate を実行します。
w = 5; N_A_withfrest = zeros(size(N_A)); for ct = 1:numel(A) in = frest.Sinestream('Frequency',w,'Amplitude',A(ct)); sysest = frestimate(mdl,in,io); N_A_withfrest(ct) = real(sysest.resp); end
周波数応答の推定結果を記述関数と共にプロットします。
plot(A,N_A,A,N_A_withfrest,'r*') xlabel('Amplitude') ylabel('N_A(A)') title('Describing Function for Saturation Using frestimate') legend('Describing function','Frequency response estimate')
モデルを閉じます。
bdclose(mdl)
周波数範囲に対して閉ループの記述関数の解析を実行することもできます。この解析のモデルを開きます。
mdl = 'scdsaturationDFcl';
open_system(mdl)
まず、記述関数を使用して、参照から出力への周波数応答を解析的に計算します。これを実行するには、参照の振幅と周波数を考慮して、最初に、非線形性への入力信号の振幅を計算します。非線形性の入力振幅は、必ずしも参照の振幅と等価ではありません。
L = zpk([],[0 -1 -10],1); w = logspace(-2,2,50); A_DF = zeros(numel(A),numel(w)); for ct_amp = 1:numel(A) for ct_freq = 1:numel(w) % Compute the input amplitude to the nonlinearity by solving the % analytical equation. opt = optimset('Display','off'); A_DF(ct_amp,ct_freq) = ... fzero(@(A_DF) solveForSatAmp(A_DF,L,w(ct_freq),A(ct_amp)),... A(ct_amp),opt); end end
次に、記述関数を使用して参照から出力への閉ループ システムの解析的な周波数応答を、振幅ごとに計算します。結果を frd オブジェクトの配列に格納します。
L_w = freqresp(L,w); for ct = 1:numel(A) N_A = saturationDF(0.5./A_DF(ct,:)); cl_resp = N_A(:).*L_w(:)./(1+N_A(:).*L_w(:)); cl(1,1,ct) = frd(cl_resp,w); end
飽和の記述関数解析と同様の方法で、frestimate を使用して閉ループ システムの周波数応答を取得します。
io(1) = linio('scdsaturationDFcl/r',1,'input'); io(2) = linio('scdsaturationDFcl/Linear',1,'output'); for ct = 1:numel(A) in = frest.Sinestream('Frequency',w,'Amplitude',A(ct),... 'NumPeriods',10,'SettlingPeriods',7); cl_withfrest(1,1,ct) = frestimate(mdl,in,io); end
解析的に計算された閉ループ振幅を frestimate からの結果と共にプロットします。想定されたとおり、結果は一致します。矢印は振幅の増加の方向を示します。
h = figure; bodemag(cl,'b',cl_withfrest,'r') annotation(h,'textarrow',[0.64 0.58],[0.64 0.58],'String','Increasing A'); legend('Analytical result','Frequency response estimate',... 'Location','southwest')
モデルを閉じます。
bdclose(mdl)
